Properties of Operations: Multiplication

Properties of Operations are those three pesky words that reoccur throughout the common core standards.  Some of you may be wondering exactly what they mean.  Properties of Operations are the foundation of arithmetic; we use them when performing computations and recalling basic facts.

In this post, I will focus on the following 3 properties that are used with addition and multiplication:

• Commutative Property
• Associative Property
• Distributive Property

Let's take a closer look at how the properties relate to multiplication. 

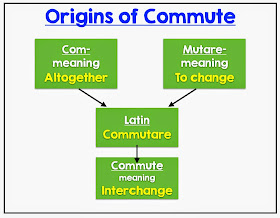
The commutative property states that changing the order of the factors does not change the product.  The root word of commutative is commute or interchange (refer to the chart below). I know that maybe too much information...... but I thought it was interesting.

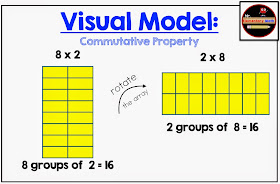
The commutative property can be very confusing to students, such as in the example 8 x 2 = 2 x 8.  Although both equations represent the same amount or product, representing them with a visual model looks different (eight groups of two versus two groups of eight).  See below.

An idea to help with the commutative property may be:

• Providing students with tiles or counters and asking them to model 8 x 2 & 2 x 8;  3 x 4 & 4 x 3,  5 x 3 & 3 x5.  Then ask the students to compare the product of each factor pair (ie. 8 x 2 and 2 x 8).  Students should be able to explain that the products are identical.  To sum it up, students should model, model, model multiplication equations in any order to see if the products are always identical.

Next, the associative property states that changing the grouping of the factors does not change the product. This property works closely with the commutative property because we often change the order of groupings of factors when multiplying numbers to make it easier to solve problems.

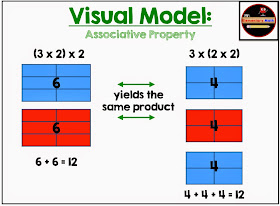
Using 3 x 2 x 2 as the basis of our groupings, below you will see a visual model of how the associative property works.

An idea to help with the associative property may be:

• Providing the students with counters or tiles and asking them to model (3 x 2) x 2 and then 3 x (2 x 2); like the example above.  From this point allow the students to determine patterns they notice.  Consider asking the students: What is the product of both expressions?  Why do they think the product is the same for both?  Try this investigation with different expressions including:  (5 x 2) x 2 and 5 x (2 x 2), (3 x 4) x 2 and 3 x (4 x 2).  Students should begin to generalize that changing the groupings does not change the product. 

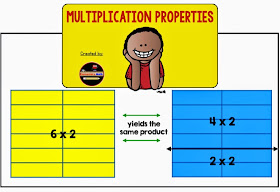
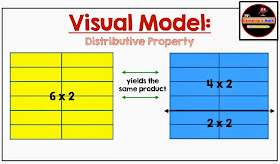
Last but certainly not least is the distributive property. The distributive property basically lets us spread out the factors so that the numbers are easier to work with.  We use this a lot when multiplying mentally.  For example, if asked to mentally find the product of 54 x 3, many of us would decompose 54 into 50 and 4.  We could then say that (50 x 3) + (4 x 3) = 150 + 12 = 162.  

Check out the visual model of distributive property below:

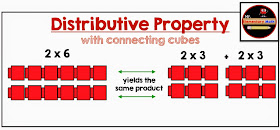
An idea to help with the distributive property may be:

• Asking students to model 2 groups of 6 (2 x 6) using connecting cubes and find two hidden facts inside of 2 x 6 like 2 x 3 and 2 x 3. Allow the students time to discover as many hidden facts inside of the 2 x 6 that they can.  Try this out with different multiplication facts through 10 x 10. Do not forget to ask students what they notice as they are doing this investigation.

Click Here to Download Your Quick Reference Sheet

Multiplication properties can seem tough, but with scaffolded support our students can definitely get it.  Consider how people use these properties in every day life to figure out problems (i.e. when shopping). As students grasp the properties, they will become better mathematicians!